FACTOR COMUN EN GRUPOS
Definición:
El factor común por agrupación de términos es un procedimiento algebraico que permite escribir algunas expresiones algebraicas en forma de factores. Para lograr este objetivo, primero hay que agrupar convenientemente la expresión y observar que cada grupo así formado tenga, en efecto, un factor común.
Por ejemplo supongamos que se necesita factorizar la siguiente expresión:
2x2 + 2xy – 3zx – 3zy
Esta expresión algebraica consta de 4 monomios o términos, separados por signos + y –, a saber:
2x2, 2xy, -3zx, -3zy
Observando con detenimiento, la x es común a los tres primeros, pero no al último, mientras que la y es común al segundo y al cuarto, y la z es común al tercero y al cuarto.
Así que en principio no existe un factor común a los cuatro términos a la vez, pero si se agrupan como se va a mostrar en el apartado siguiente, es posible que sí aparezca uno que ayude a escribir la expresión como el producto de dos o más factores.
Ejercicio de ejemplo:
Factorizar la expresión: 2x2 + 2xy – 3zx – 3zy
Paso 1: Agrupar
2x2 + 2xy – 3zx – 3zy = (2x2 + 2xy) + (-3zx – 3zy)
Paso 2: Sacar el factor común de cada grupo
2x2 + 2xy – 3zx – 3zy =
=(2x2 + 2xy) – (3zx + 3zy) =
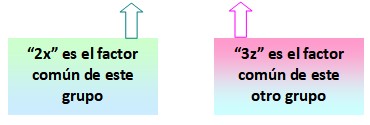
=2x (x+y) – 3z (x+y)
Importante: el signo negativo también es un factor común que debe ser tomado en cuenta.
Ahora nótese que el paréntesis (x+y) está repetido en los dos términos obtenidos al agrupar. Ese es el factor común que se estaba buscando.
Paso 3: Factorizar toda la expresión
2x2 + 2xy – 3zx – 3zy = (x+y) (2x – 3z)
Con el resultado anterior se ha llegado a la meta de la factorización, que no es otra que transformar una expresión algebraica a base de sumas y restas de términos, en el producto de dos o más factores, en nuestro ejemplo, de: (x+y) y (2x – 3z).
OTROS EJEMPLOS
1) ax+ay+bx +by =
ax +bx +ay +by =
x(a+b) + y(a+b) =
(x+y)(a+b)
4.(a + b) + x.(a + b) =
(a + b).(4 + x)
a.(4 - 7x2 + y) + z.(4 - 7x2 + y) =
(4 - 7x2 + y).(a + z)

Comentarios
Publicar un comentario